斩波放大器:理论研究笔记
提到斩波,第一反应总是电力电子中的斩波。
但实际上这一说法并不只在升降压变换中使用,在运算放大器中也有一类神奇的分支,叫做斩波运算放大器。
本篇文章接下来就将简要讲解关于斩波放大器的相关理论,如有疏漏,还望指正。
稳定精密
在一些精密电路设计的情景中,通常会对运放的失调和漂移提出很高的要求。
如果寄希望于集成电路的进步来提高性能,可能最终等来的只会是高昂的成本。然而如果通过模拟信号处理的方式解决,或许可以有更好的解决方法。
在数十年前,工程师们就面临着这样的问题,于是斩波放大器应运而生,在当时的工艺上进一步降低了失调和温漂。
在 ADI 的一篇应用指南 MT-055 中提到,当时最好的双极性放大器的失调电压为 25μV ,漂移为 0.1μV/°C 。然而如果使用斩波运放,就能将失调进一步降低到 5μV 以及更小的失调漂移[1]。
原理分析
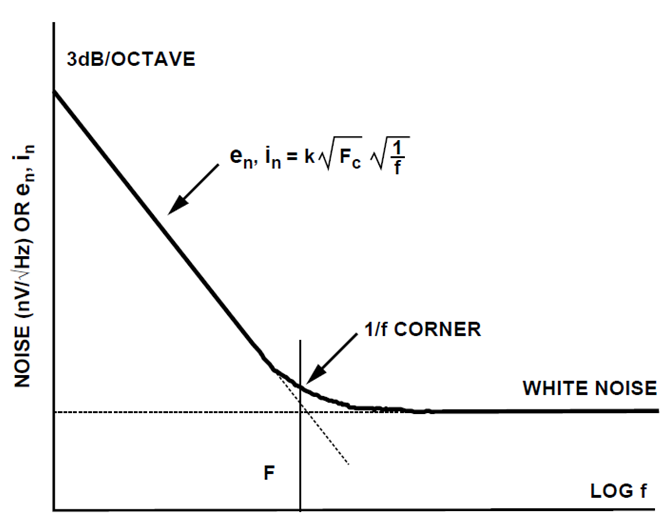
1.本底噪声
在深入讲解原理前,先简要说明一下,在精密测量领域,主要存在两类噪声干扰,一类是电路干扰,另一类是本底噪声。
电路干扰可以通过技术手段尽可能削弱。但闪烁噪声是元器件的固有效应,不仅难以过滤,且功率谱密度随着频率的降低反而会增大。意味着在直流或低频信号处理中,它会直接叠加在有用信号上,难以通过常规滤波手段根除。
2.自稳零与斩波
那么斩波结构是如何抑制这些干扰的呢?
首先要提到的是,目前的斩波运放包含了两种不同的技术,分别是自稳零与斩波。他们都有斩波过程,但在原理上大不相同,所以它们更适合被统称为零漂放大器。
所以本文接下来就会严格区分两类运放,自稳零运放和斩波运放,不再混淆说明为斩波放大器。
我们先从自稳零讲起,先来看一张图,展示了经典的自稳零运放构成。
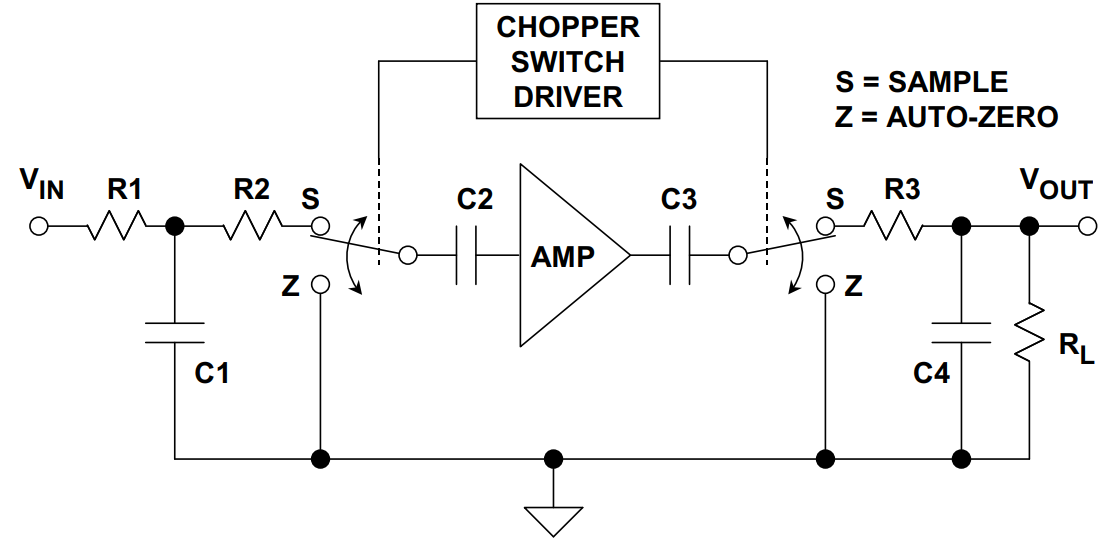
整体电路由 CHOPPER SWITCH DRIVER 控制,在运放输入输出端都增加了开关以及串联电容。
当开关处于 Z 时,电容 C2 直接对地,采样并存储了此时的失调电压误差,使得在正确的信号回路时,该误差可以被电容电压抵消,这样就实现了抑制运放自身偏置。此时输出端也执行相同动作,将输出偏置降到最低。当开关接回 S 时,形成输入通路,此时的整个通路上的偏置是趋于零的,这样就达到了我们的目的。这就是自稳零作用,但是单单是自稳零对于 1/f 噪声的抑制并不彻底。
不过这真的是个很巧妙的方法对吧,然而仔细想想就会发现其实并不合理,到底是哪里不合理呢?既然采用电容平衡偏置,那么电容充放电的间隔是多少,如何界定?开关难道不会引入额外的噪声?既然有开关频率限制,那这样的运放还剩下多少的有效带宽?更致命的是,这种采样处理方式是否会把高频噪声折叠到基带,反而搞砸了原本干净的信号?
这些新的问题我们暂且按下不表,继续剖析斩波的核心原理。
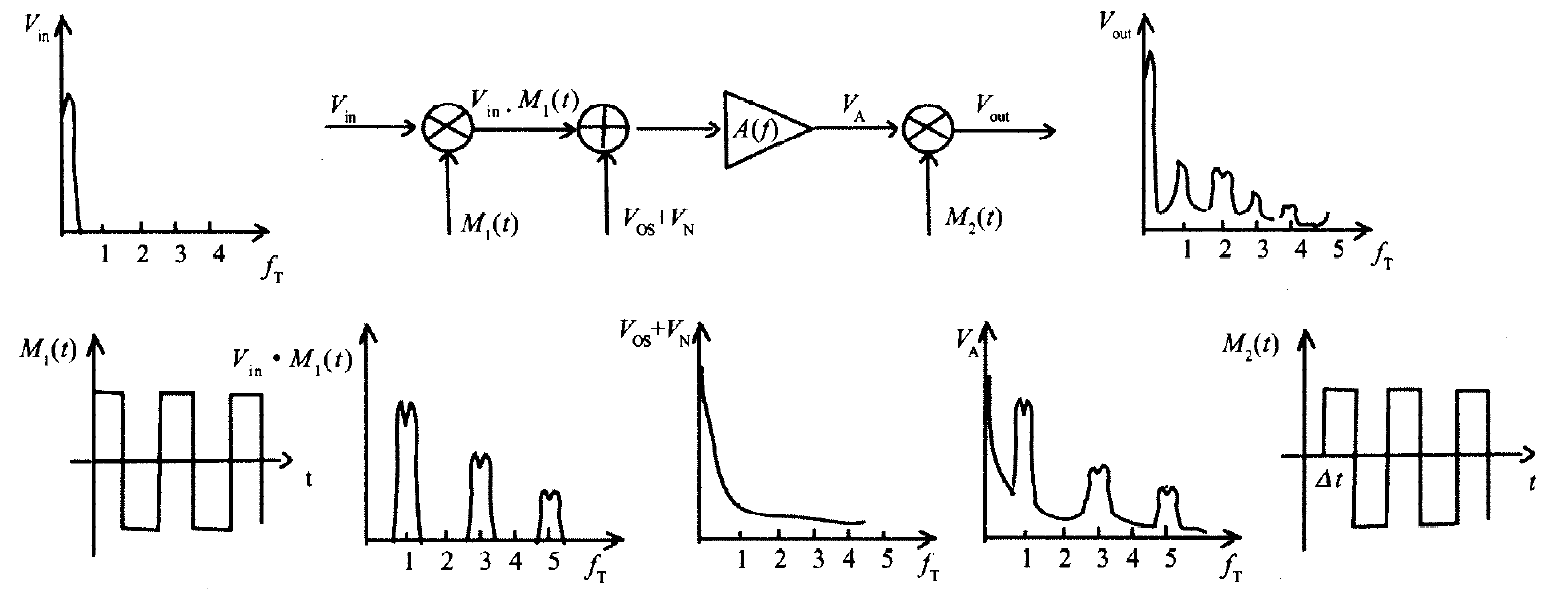
如果说自稳零是靠电容存储来减去偏差,那么斩波则是进行更高级的频谱搬移。
例如流程图的左上角,信号 $V_{in}$ 的频谱原本分布在极低频段,接下来通过与方波 $M_1(t)$ 相乘,实现频谱搬移。然后再叠加 $V_{OS}+V_N$ 即运放的偏置与噪声,结合成 $V_A$ 的频谱。最后在输出端,经过方波 $M_2(t)$ 的解调,原信号的频谱返回到初始位置,而噪声信号被搬移至更高频,接下来只需要低通滤波器的处理,就可以移除噪声的影响。
经历了两次方波相乘(调制+解调),相当于乘以 $M_1(t) \cdot M_2(t)$。因为两者同步,结果为 1,所以信号回到了原位。而噪声只经历了一次相乘(解调),所以从直流(DC)被搬移到了方波频率及其奇次谐波上。
如果觉得不够直观,还可以看下图中的仿真结果[2]:
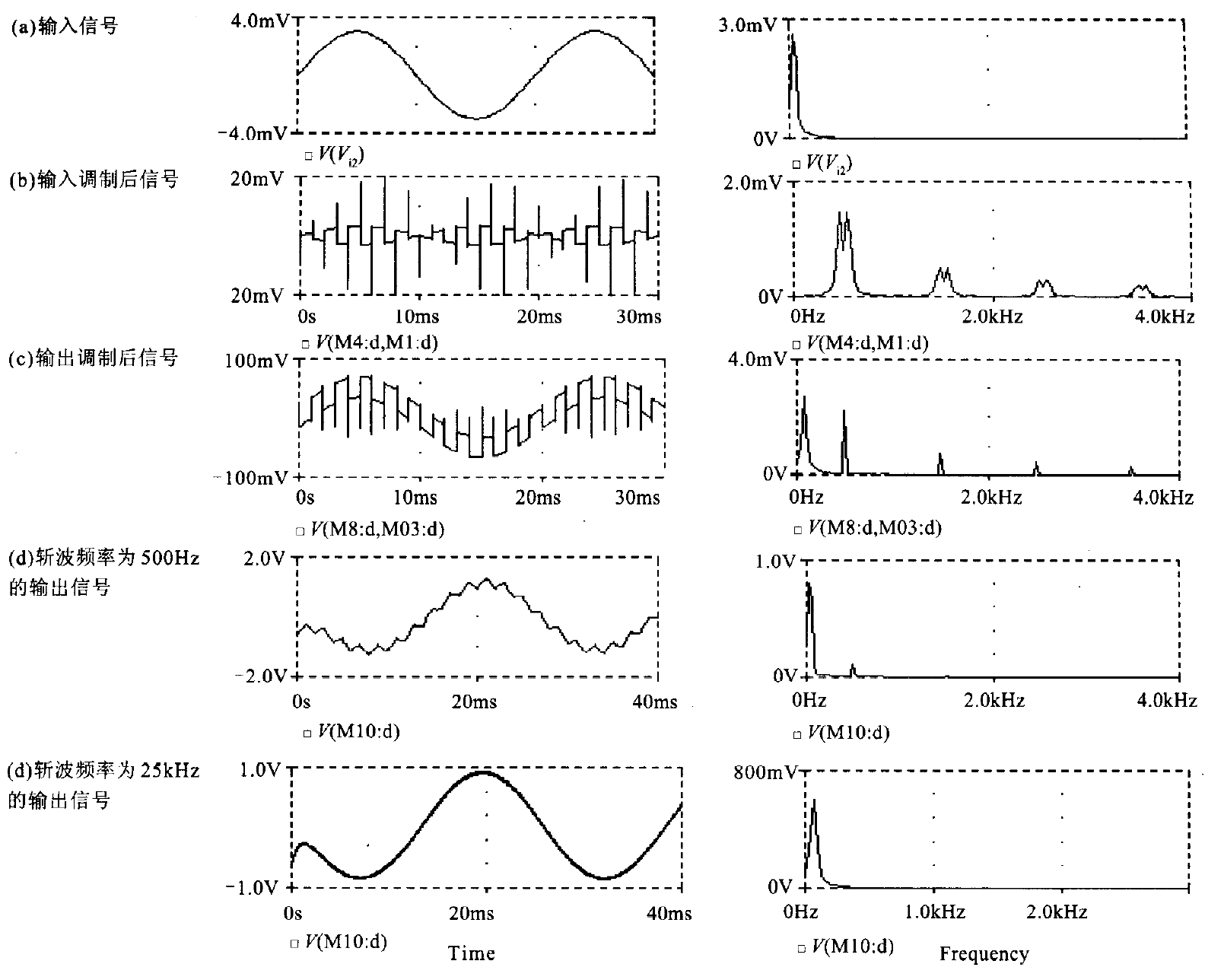
从全流程的频谱变化中,可以清晰看到每一步流程的清晰变化,从一个单纯的正弦波再到被方波相乘,再到被解调,然后配合滤波器后得到更加理想的正弦频谱。而且对比最开始的频谱和最终的频谱,可以看到尖峰更加独立,而非紧贴着纵轴。也就是说,放大后的正弦摆脱了偏置和 1/f 噪声的影响。
3.斩波并非完美
讨论了这么多内容,其实斩波技术也并非灵丹妙药,它在解决旧问题的同时,也带来了不少新麻烦。
首先,开关调制会引入时钟馈通,会在信号通路上产生新的斩波纹波。如果处理不好,这些纹波甚至会直接掩盖掉你想测量的微弱信号。
其次,开关频率受限于运放本身的带宽与稳定性。斩波频率无法无限提高,意味着它对高于斩波频率的噪声抑制能力有限。同时,为了保证信号在开关切换瞬间能够准确建立,你必须在带宽与功耗之间做出艰难的取舍。
因此,实际设计中,常在斩波架构外增加纹波抑制电路、自动校准环路或是辅助放大器,以平衡性能与复杂度。
关于前面在分析过程中提到的问题,我们会注意到:自稳零使用采样保持技术,由于噪声折回基带,其带内电压噪声较大,这确实是难以弥补的缺陷。而斩波使用信号调制和解调技术,具有更低的基带噪声,但在斩波频率及谐波处产生噪声频谱。因此,斩波放大器更适合直流或低频应用,自稳零放大器则更适合宽带宽应用[3]。
在实际应用中,为了兼顾低频噪声与带宽性能,许多高性能精密运放会采用斩波与自稳零结合的架构,或在斩波核心外增加辅助高速通路,以在抑制漂移与噪声的同时,拓展可用带宽。
简单总结
斩波技术是一种用于精密测量的有效方式,它通过自稳零与调制-解调机制,将工艺和器件本身的低频噪声滤除,从而在常规工艺基础上实现了接近理论极限的直流精度。尽管仍有不足,但在传感器信号采集、医疗仪器、高精度检测等要求极致失调与低温漂的领域,它仍是不可或缺的关键技术之一。