锁相放大器：理论研究笔记

最近重新整理之前做过的电赛题目资料时，回忆起了这个有趣的话题。

所谓锁相放大器，就是能够在一片噪声的干扰之中正确找到目标信号，并对其进行分离和增益的一种放大器。

听起来相当魔幻对吧，实际上这样的电路实现起来也确实会困难重重，条件非常苛刻。但是锁相放大器依然还是有很丰富的理论研究价值，接下来就来进行分析。

原理

锁相放大器，英文全称Lock-in Amplifier，又称LIA。

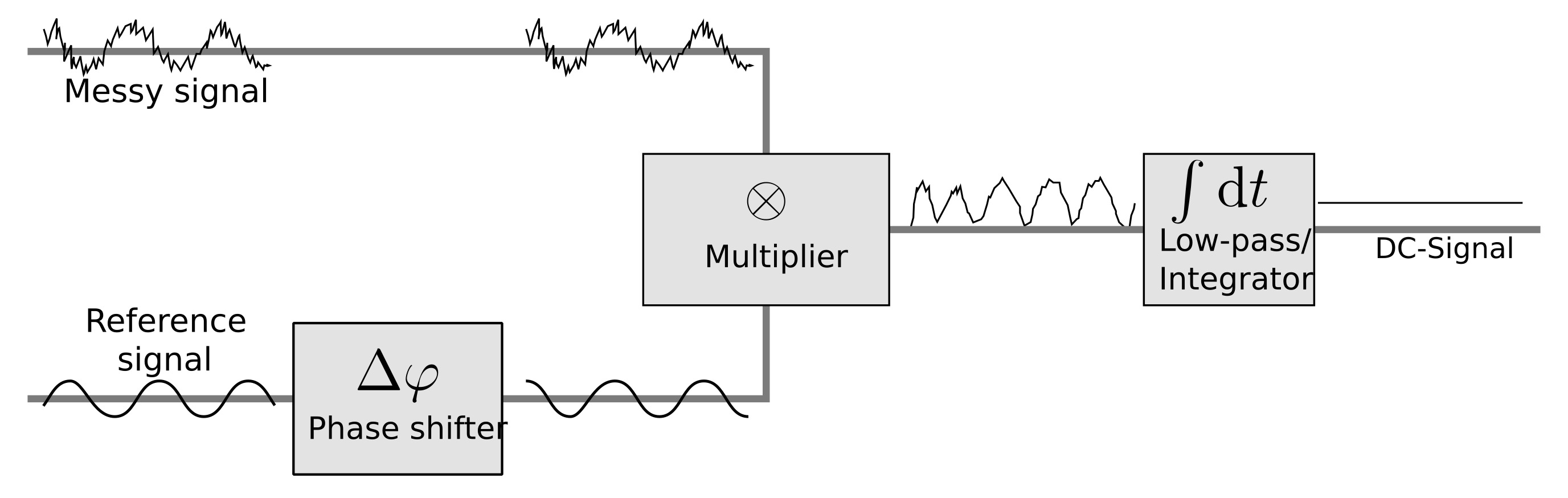
利用三角函数积化和差的思想，产生一路正弦信号与输入信号相乘，得到如下结果：

$$ \begin{align} &A_1\sin(\omega + \varphi) \cdot A_2\sin(\omega + \varphi) \\ &= \frac{1}{2} A_1 A_2 \{\cos[(\omega + \varphi) - (\omega + \varphi)] - \cos[(\omega + \varphi) + (\omega + \varphi)]\} \\ &= \frac{1}{2} A_1 A_2 \left[1 - \cos(2\omega + 2\varphi)\right] \end{align} $$

只要保证正弦信号与目标信号同频同相，就能得出直流信号与两倍频的叠加波。

然后利用低通滤波器滤除 $ -\frac{1}{2} A_1 A_2 \cos(2\omega + 2\varphi) $ ，得到直流分量 $ \frac{1}{2} A_1 A_2 $ 。

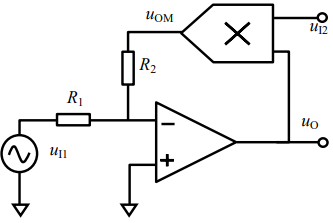
对于该直流分量的处理就简单了，因为 $ A_1 $ 是已知信号，利用除法器即可将 $ A_2 $ 准确还原出来。
（提示：图中右上角的元件是乘法器，$ U_{I1} $ 和 $ U_{I2} $ 是输入电压，$ U_{O} $ 是除法结果，即利用乘法器和运放即可搭出除法器电路）

或者直接将信号采样到单片机，再在内部进行除法运算，即可得到目标信号的采样数据。

相位差问题

有人可能会疑惑，这不是多此一举吗，既然我都知道目标信号的频率了，做这个还原有什么意义？

其实并不是这样。

首先我们先规定一下，需要还原出来的信号叫做“目标信号”，本地产生的信号的叫“参考信号”。

在实际应用中，虽然不能得知目标信号具体的频率，但我们可以在一个范围内扫频来逼近目标频率。

所谓扫频就是用频率步进变化的正弦波去逐次逼近结果，只有频率接近目标信号时，锁相放大器的结果才会达到绝对值最大，此时才能确定目标信号的频率。

这里就可以将上面的公式推广到一般情况。

$$ \begin{align} &A_1\sin(\omega_1 + \varphi_1) \cdot A_2\sin(\omega_2 + \varphi_2) \\ &= \frac{1}{2} A_1 A_2 \{\cos[(\omega_1 + \varphi_1) - (\omega_2 + \varphi_2)] - \cos[(\omega_1 + \varphi_1) + (\omega_2 + \varphi_2)]\} \end{align} $$

注意到，当 $ \omega_1 + \varphi_1 $ 与 $ \omega_2 + \varphi_2 $ 极为接近时，两者相减结果趋于0，使得 $ \cos $ 趋近于1，也就可以将 $ \frac{1}{2} A_1 A_2 \cos[(\omega_1 + \varphi_1) - (\omega_2 + \varphi_2)] $ 近似看作直流分量。

不过这里只能说是“趋近”，而不能是达到完全相等。因为尽管待测信号源输出的是 $ 1khz $ 的正弦波，系统主动输出的也是 $ 1khz $ 的正弦波，由于时钟源的差异，两者几乎不可能做到完全同步。频率之差可能最开始很小，但随着时间推移，两者的相位最终会逐渐错开。况且常见时钟源受到电压、温度等因素影响都比较大，因此频率偏移是一个重要因素。

这时就需要再次扫频校准，带来了麻烦，那么能不能有合理的办法解决呢？

双相位法

在《新概念模拟电路》的相关章节中（第四册 P231 电荷放大器和锁定放大器）就提到了双相位法。

双相位法在原先的基础上，增加了一路同频的参考信号来进行相乘，但该信号需要进行90°的相移。

然后再将两路正交的正弦波分别相乘并滤波，得出 $ U_{O1} $ 和 $ U_{O2} $ 两路信号。

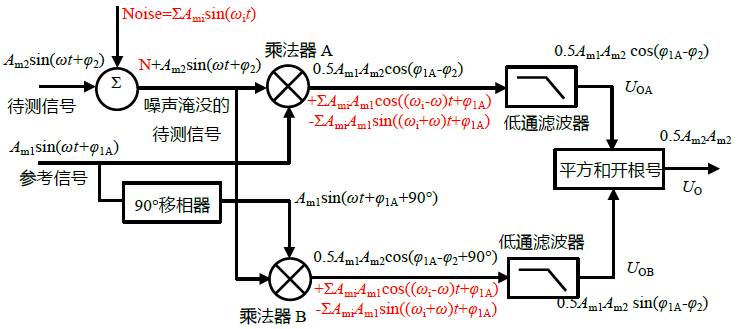
系统最终会得到 $ U_{OA} $ 和 $ U_{OB} $ 两个分量，这两者虽然不是我们想要的的直流分量，但是将其平方和开根就可得到新的结果 $ U_O $ ：

$$ \begin{align} U_O &= \sqrt{U_{OA}^{2} + U_{OB}^{2}} \\ &= \frac{1}{2} A_{m1} A_{m2} \sqrt{\sin(\varphi_{1A} - \varphi_2)^2+\cos(\varphi_{1A} - \varphi_2)^2} \\ &= \frac{1}{2} A_{m1} A_{m2} \end{align} $$

由此就可在相位关系未知的情况下得出直流分量 $ \frac{1}{2} A_{m1} A_{m2} $ 的值，这样就巧妙的解决了上述问题。

（注意书上图片中最终结果有误，写成了 $ U_O = \frac{1}{2} A_{m2} A_{m2} $，这里应该只是笔误）

不仅如此，我们还可根据 $ U_{OA} $ 和 $ U_{OB} $ 的关系求出待测信号的相位差：

$$ \tan(\varphi_{1A} - \varphi_2) = \cfrac{\sin(\varphi_{1A} - \varphi_2)}{\cos(\varphi_{1A} - \varphi_2)} = \cfrac{U_{OA}}{U_{OB}} $$

接下来只需要利用 $ \arctan(\cfrac{U_{OA}}{U_{OB}}) $ 就可得到相位差。

实在是太神奇了。

双相位法真是一种非常巧妙的解决办法，我们不需要严格匹配目标的相位与实际的相位，就能准确求出直流分量，甚至还能顺带求出相位差。而原理也并不复杂，仅仅是掌握三角变换的特性就能轻松理解。

这些三角变换并不困难，甚至只需要初高中的水平就能推导得出。但当其与电路设计结合在一起时，还是不得不佩服这些数学家的小把戏。

上述内容针对锁定放大器的原理进行了改进，但是在实际应用的过程中还会遇到新的问题，接下来就来看看实践改进应该如何分析？

改进

在实践部分，书中提到了移相时会遇到的问题。

上述方法，理论分析头头是道，但实现起来很困难。其中最大的难点在于90°移相。我们知道，全通滤波器可以实现移相，但它的标准功能是，对不同频率实施不同的移相而要对任意给定的频率都能实现90°相移，且幅度不发生变化，在模拟电路中是很难做到的。

书中以模拟电路的视角来考虑相位问题，确实不太容易实现移相。但如果从实际应用的角度，在一些要求没那么高的场合，完全可以考虑利用多通道DDS直接设置两路正交的正弦波来解决这个问题，因此这里可能并不是最困难的地方。

但在另一方面，双相位法需要两路相同的乘法器电路来实现，而乘法器本身就是价格昂贵且使用条件比较苛刻的精密元件，很多情况下都没有机会用上这么奢侈的方案。那么有没有办法能替代掉呢？

还真有。

将正弦信号替换为方波信号，就能达到相同的效果。

仔细思考一下这套系统中的难点如何解决：

• 首先参考信号要易于产生和调相，方波信号其实就是0和1的周期性变换，非常易于产生和调相。

• 其次就是方波可以在一定程度上等效于乘法：如果我们之间将方波与任意信号相乘，会发现其实当方波为1时，结果就是任意信号本身；而当方波为0时，乘法结果也就是零。

这个效果似乎很眼熟？

这不就是模拟开关的效果了吗？

也就是说利用方波控制模拟开关，再间接控制输入信号导通，能达到与乘法器同样的效果。

接下来给出方波双相位法的示意图：

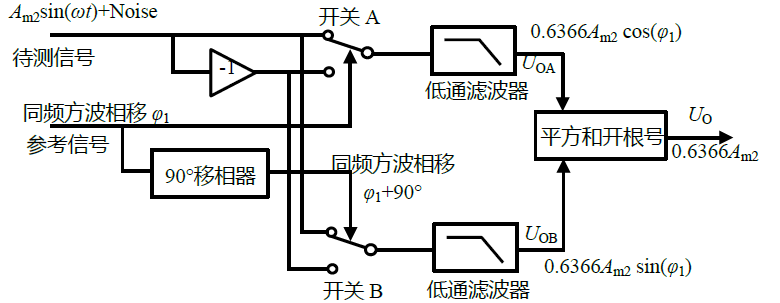
这里的大体思路还是与原方案相同，都是将输入信号与待测信号做乘法，将低通滤波后的结果进行平方和开根号，即可得到最后的 $ U_O $ 。

只是在如下这些细节部分有所不同：

1. 首先是方波与正弦波相乘结果的直流系数不太相同，达到了0.6366（图中 $ A_{m1} = 1 $ ）

2. 其次方波相乘并不能直接等效于乘零，而是应该接上反相器，等效为一个正负对称的方波。

不过上述细节并不影响方案的整体思路，系数的差异可以通过放大器系数的调节解决。

其中关于直流系数的差异，即0.6366到底是怎么得出的，有兴趣的可以自行在书中寻找推导过程，这里并不做深入讨论。